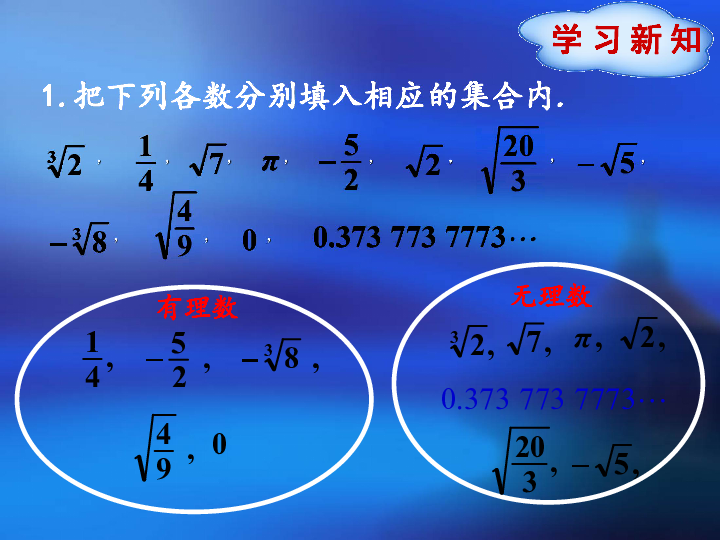
啥是有理数和无理数

*** 次数：1999998 已用完，请联系开发者***

╯＾╰ 圆周率π的奥秘:无理数还是有理数?绝无可能!其原因显而易见,π已被数学家们证实为无理数,且证明过程并非极其复杂。对于感兴趣的朋友而言,简单搜索即能获得答案,此处便不再赘述。 因此,既然π已被确证为无理数,那么它就必然是无理数,而非有理数!然而,许多人对π作为无理数这一事实仍感困惑。 在数学定义中,π即...

(＊?↓˙＊)

π是无理数,圆的周长也应该是无理数,意味着圆周长不能是整数?这条线段当然是有长度的,而且长度是固定的,这点没有疑问吧? 但是这个固定的长度并不一定是有理数,也可能是无理数,而且是无理数的可能性更大,因为无理数远比有理数多得多。尽管有理数和无理数都有无限多个,但无限也有大小之分,无理数的无限就远大于有理数的无限! 不要说所有...

∪ω∪ π是无理数,意味着圆周长也是无理数,难道圆周长不能是整数吗?所有有理数和无理数构成了实数系,数轴上的每一个点都对应着一个实数。如果你可以在数轴上随意切割,那么得到的点更可能是无理数,因为它们的数量要远远多于有理数。而在数轴上表示π其实也很简单,一种简单的方法是: 画一个数轴。 画一个直径为1的圆,从原点O开始,沿着x轴滚动...

∪＾∪

(^人^) 揭秘圆周长之谜:π为无理数,圆周长度是否注定非整数?这条线段当然是有长度的,且长度是固定的,这一点应该毫无疑问吧? 不过,这个固定的长度不一定是有理数,也可能是无理数,而且更有可能是无理数。因为无理数远比有理数多得多。尽管有理数和无理数都有无限多个,但无限也是有大小之分的,无理数的无限要远远超过有理数的无限。 不要...

＞▽＜

知识科普:圆周率π有没有可能根本就不是无理数?没有任何可能性!原因很简单,数学家们早就证明了π确实是无理数,证明过程并不太复杂,这里不再详述,有兴趣的简单搜索就能找到答案! 所以,既然已经证明了π是无理数,它就是无理数,不可能是有理数!不过很多人对π是无理数感到有些不解。 数学上的定义,π就是圆周长与直径的比,圆周...

圆周率与有理数的奇妙邂逅:乘法中的神秘转变大揭秘!(例如有时被认为是3.14而有时又被视为3.15),才能说明它不是恒定不变的量。然而事实并非如此。 此外,为了使圆的周长与其直径之间保持固定的比例关系,至少其中之一必须是无理数。这意味着在任意给定长度的线条中,虽然该长度可能是有理数也可能是无理数,但从概率角度来看,成为...

圆周长的奥秘:π的无理性揭示了什么?所有有理数和无理数构成了实数系,数轴上的每一个点都对应着一个实数。如果你可以在数轴上随意切割,那么得到的点更可能是无理数,因为它们的数量要远远多于有理数。而在数轴上表示π其实也很简单,一种简单的方法是: 画一个数轴。 画一个直径为1的圆,从原点O开始,沿着x轴滚动...

（°ο°）

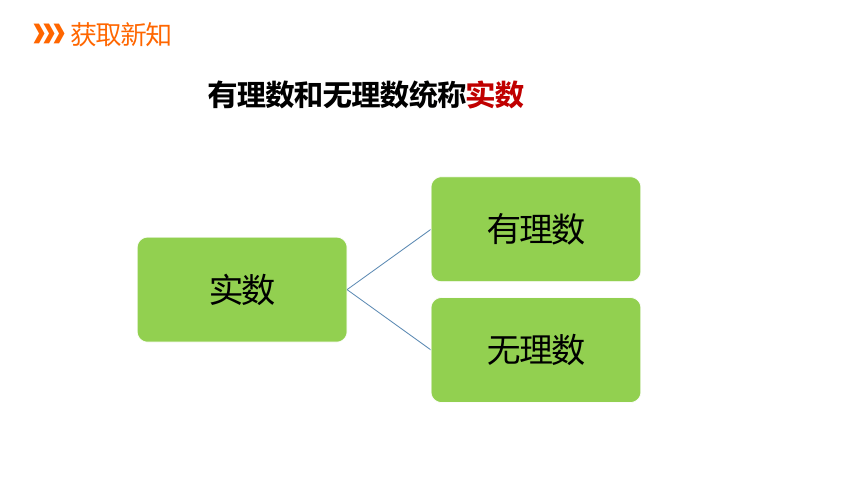
＞＾＜ 一米长棍子能精确三等分吗?探秘除不尽的数学谜题在数学的广阔领域中,实数这一大家庭包含了有理数和无理数两大分支,它们与数轴上的点一一对应,形成了井然有序的体系。 然而,我们对于“无理数”这个词汇似乎总有一种误解,常常将其与“不合理”联系在一起。实际上,无论是无理数还是有理数,都是实数的重要组成部分,它们都代表...

1/3等于0.333循环,那1米长棍子能否分三等份呢?我们常常会在潜意识里认为无理数是“不合理”的数。但实际上,有理数和无理数在本质上是等价的,它们都是真实存在的数,都是明确无误的数。 由于无理数具有无限不循环的特性,对于一些人来说,接受“无限”这一概念存在一定的难度。即使是有理数以无限循环的形式呈现,也让人难以...

揭秘:当1/3等于0.333循环时,一米长的棍子能否完美三等分?往往我们会潜意识地以为无理数是“不合理”的数。但其实,有理数和无理数都是等价的,它们都是实实在在存在的数,都是明确的数。 由于无理数表现为无限不循环的性质,对一些人来说,接受无限的概念似乎有些困难。即便是有理数的无限循环表示也让人不易理解。 例如,有人会提出这...

ˇ▂ˇ